With this method, the soil is modeled as a series of discrete elements, which we will call "slices", and takes into account the mutual compatibility between the slices. A slope in the present model is treated as comprised of slices that are connected by elastoplastic Winkler springs. One set of springs is in the normal direction to simulate the normal stiffness. The other set is in the shear direction to simulate the sliding resistance at the interface. The behavior of the normal and shear springs is elastoplastic. The normal springs do not yield in compression, but they yield in tension, with a small tensile capacity for cohesive soil (tension cutoff) and no tensile capacity for frictional soil.

 

 

 

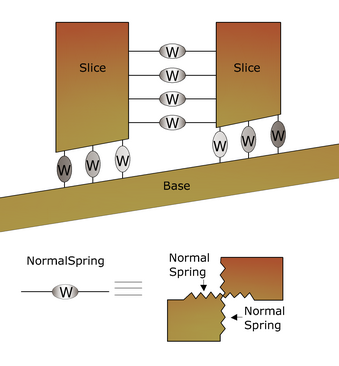
Σχηεματιχ ϕιγυρε οϕ Ωινκλερ σπρινγσ ατ τηε ιντερϕαχε βετωεεν τωο

αδφαχεντ σλιχεσ ορ βετωεεν σλιχε ανδ ιμμοϖαβλε βασε

 

The shear springs yield when the shear strength is reached, and two types of behaviours are distinguished: brittle soil and nonbrittle soil. For brittle soil, the peak strength of the shear springs is determined by:

 

 

While the residual shear strength is given by:

 

 

For simplicity, in the following analysis, it is assumed that after reaching the peak strength, the soil resistance drops immediately to the residual strength value.

For plastic nonbrittle soil, the strength does not reduce at large shear deformation; thus, the residual strength has the same value as the peak strength. The formulation of the present method follows that of previous research of Chang and Mistra on the mechanics of discrete particulates.

 

 

© GeoStru Software