Hoek & Bray

For rock slopes, different from those in soil, the Mohr-Coulomb failure criterion can not be used to define the resistance of the material; however with this method is described a procedure that allows the application of the classical methods of Limit Equilibrium even in rocky slopes.

In this purpose are defined the angle of shearing and the cohesion along the sliding surface according to the following expressions:

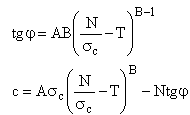
where:

σc is the uniaxial compressive strength of the rock;

A, B, T constants function of the lithotype and the quality of the rock (table below);

N normal stress at the base of the slice.

The constants A, B and T are determined as a function of the classification of the rocks according to Bieniawski (RMR index) or according to Barton (Q index).

Between the two classifications, on the base of 111 examples analyzed, was found the following correlation:

Lithotype Rock quality	Limestones Dolomites Marl	Shales Siltstones	Arenites Quartzites	Andesites Basalts Rhyolites	Amphibolites Gneiss Granites Gabbros
RMR =100 Q = 500	A = 0.816 B = 0.658 T = -0.140	A = 0.918 B = 0.677 T = -0.099	A = 1.044 B = 0.692 T = -0.067	A = 1.086 B = 0.696 T = -0.059	A = 1.220 B = 0.705 T = -0.040
RMR = 85 Q = 100	A = 0.651 B = 0.679 T = -0.028	A = 0.739 B = 0.692 T = -0.020	A = 0.848 B = 0.702 T = -0.013	A = 0.883 B = 0.705 T = -0.012	A = 0.998 B = 0.712 T = -0.008
RMR = 65 Q = 10	A = 0.369 B = 0.669 T = -0.006	A = 0.427 B = 0.683 T = -0.004	A = 0.501 B = 0.695 T = -0.003	A = 0.525 B = 0.698 T = -0.002	A = 0.603 B = 0.707 T = -0.002
RMR = 44 Q = 1	A = 0.198 B = 0.662 T = -0.0007	A = 0.234 B = 0.675 T = -0.0005	A = 0.280 B = 0.688 T = -0.0003	A = 0.295 B = 0.691 T = -0.003	A = 0.346 B = 0.700 T = -0.0002
RMR = 3 Q = 0.1	A = 0.115 B = 0.646 T = -0.0002	A = 0.129 B = 0.655 T = -0.0002	A = 0.162 B = 0.672 T = -0.0001	A = 0.172 B = 0.676 T = -0.0001	A = 0.203 B = 0.686 T = -0.0001
RMR = 3 Q = 0.01	A = 0.042 B = 0.534 T = 0	A = 0.050 B = 0.539 T = 0	A = 0.061 B = 0.546 T = 0	A = 0.065 B = 0.548 T = 0	A = 0.078 B = 0.556 T = 0

Lithotype

Rock quality

Limestones

Dolomites

Marl

Shales

Siltstones

Arenites

Quartzites

Andesites

Basalts

Rhyolites

Amphibolites

Gneiss

Granites

Gabbros

RMR =100

Q = 500

A = 0.816

B = 0.658

T = -0.140

A = 0.918

B = 0.677

T = -0.099

A = 1.044

B = 0.692

T = -0.067

A = 1.086

B = 0.696

T = -0.059

A = 1.220

B = 0.705

T = -0.040

RMR = 85

Q = 100

A = 0.651

B = 0.679

T = -0.028

A = 0.739

B = 0.692

T = -0.020

A = 0.848

B = 0.702

T = -0.013

A = 0.883

B = 0.705

T = -0.012

A = 0.998

B = 0.712

T = -0.008

RMR = 65

Q = 10

A = 0.369

B = 0.669

T = -0.006

A = 0.427

B = 0.683

T = -0.004

A = 0.501

B = 0.695

T = -0.003

A = 0.525

B = 0.698

T = -0.002

A = 0.603

B = 0.707

T = -0.002

RMR = 44

Q = 1

A = 0.198

B = 0.662

T = -0.0007

A = 0.234

B = 0.675

T = -0.0005

A = 0.280

B = 0.688

T = -0.0003

A = 0.295

B = 0.691

T = -0.003

A = 0.346

B = 0.700

T = -0.0002

RMR = 3

Q = 0.1

A = 0.115

B = 0.646

T = -0.0002

A = 0.129

B = 0.655

T = -0.0002

A = 0.162

B = 0.672

T = -0.0001

A = 0.172

B = 0.676

T = -0.0001

A = 0.203

B = 0.686

T = -0.0001

RMR = 3

Q = 0.01

A = 0.042

B = 0.534

T = 0

A = 0.050

B = 0.539

T = 0

A = 0.061

B = 0.546

T = 0

A = 0.065

B = 0.548

T = 0

A = 0.078

B = 0.556

T = 0

Relation between the classification of the rocks and the parameters A, B and T