Computation of the Yield Moment

Calculation of the Yield Moment for a steel tubular section

The section under examination is the following:

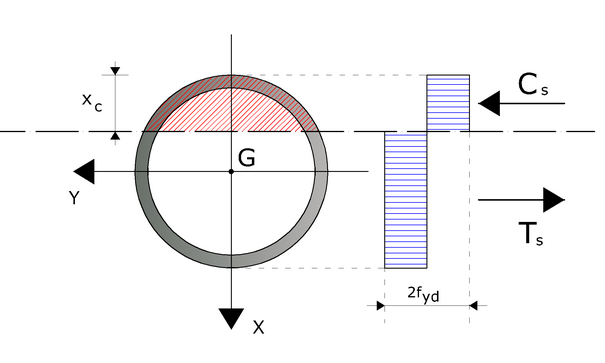
sez_acciaio

Reference diagram for the calculation of the yield moment for a steel tubular section

The calculation of the yield moment has been made assuming, for steel, a rigid-plastic constitutive bound, with limit yield stress equal to fyd. The yield moment has been determined by interpolation on the section interaction curve.

In order to construct the interaction curve of the section, the following procedure has been followed:

- step 1: Fixing the depth of the neutral axis (xc) - (starting from xc = 0);

- step 2: Calculating the resultant in terms of normal stress (Nd);

- step 3: Calculating the resultant moment (Md) as regards the geometric center of gravity of the section;

- step 4: Memorizing the calculated point (Nd, Md);

- step 5: Increasing xc, if xc is still lower than or equal to the diameter of the section, then back to step 1, otherwise the procedure is over.

Note:

In this way, the upper part of the interaction domain is constructed. In any case the lower part is identical, but hemi symmetrical.

The generic point of the interaction domain has been calculated using the following formulas:

In the previous formulas, the symbols have the following meaning:

-	Ac_s: Area of compressed steel;

-	At_s: Tensile stress steel area;

-	fcd: concrete compressive cylinder strength;

-	fyd: steel yield strength;

-	dCs :Distance between the resultant of the compression stresses of steel and the center of gravity of the section;

-	dTs :Distance between the resultant of the tensile stresses of steel and the center of gravity of the section.

Calculation of the Yield Moment for a steel tubular section immersed into a concrete circular section

The previous formulation, used for the tubular section, can be extended to the case in which the tubular section is immersed into a concrete section. In this case, it is necessary to take into account the concrete contribution, according to the following diagram:

sez_acc_calc_EN

Diagram for the calculation of the yield moment for a steel tubular section immersed in a circular concrete section

As you can observe, the concrete type considered as a reactant is only compressed concrete. The values of the stresses at a fixed depth of the neutral axis of the section is as follows:

In the previous formulas, the symbols have the following meaning:

-	Ac_s: Area of compressed steel;

-	Ac_c: Area of compressed concrete;

-	At_s: Tensile stress steel area;

-	fcd: concrete compressive cylinder strength;

-	fyd: steel yield strength;

-	dCs :Distance between the resultant of the compression stresses of steel and the center of gravity of the section;

-	dCc: Distance between the resultant of the compression stresses if concrete and the center of gravity of the section;

-	dTs :Distance between the resultant of the tensile stresses of steel and the center of gravity of the section.

Calculating the yield moment for a circular RC section

In this case too a constitutive bound of the rigid-plastic materials is assumed, with limit stresses equal to fcd and fyd for concrete and steel, respectively. The reference diagram is the following:

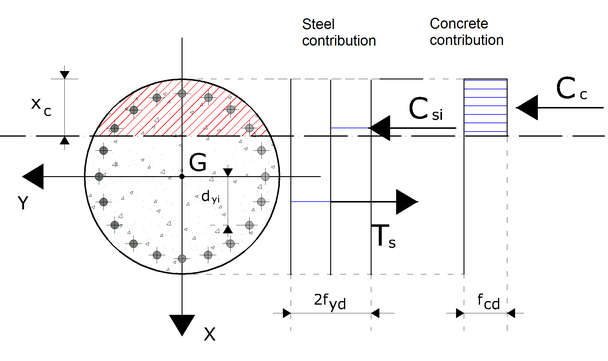
sez_c.a_EN

Diagram for the calculation of the yield moment of a circular RC section

In this case, the value of the stresses – in correspondence of a preset depth of the neutral axis – is the following:

In the previous formulas, the symbols have the following meaning:

-	Ac_c: Area of compressed concrete;

-	Asi+: Area of the i-th reinforcement bar situated above the neutral axis;

-	Asi-: Area of the i-th reinforcement bar situated under the neutral axis;

-	Asi: Area of the i-th reinforcement bar;

-	fcd: concrete compressive cylinder strength;

-	fyd: steel yield strength;

-	dCc: Distance between the resultant of the compression stresses if concrete and the center of gravity of the section;

-	dyi: is the positive distance (along the vertical) measured between the center of gravity of the i-th reinforcing bar and the center of gravity of the section