The method of Seed and Idriss (1971-1982) calculates the CSR using the following formula:

 

 

To determine the value of the reduction factor rd is used the empirical formula proposed by Iwasaki et al. (1978):

 

 

 

while for the correction factor MSF refers to the values ​​reported in Table 1 obtained by several researchers, including Seed H. B. and Idriss I. M (1982).

 

         Table 1- Scale factor of the magnitude derived from several researchers

 

 

 

The Cyclic Resistance Ratio is calculated as a function of magnitude, the number of blows in the SPT test, the effective vertical pressure and the relative density.

The graphic (Figure 2) is obtained by selecting the cases of soils where the liquefaction occurred and didn't occurred during earthquake.

Initially is calculated the corrected number of blows to the desired depth to take account of the lithostatic pressure by the following expression:

 

 

where Nm is the average number of blows in the standard penetration test SPT and CN is a correction factor that is determined by the relation:

 

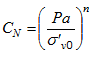
where σ'vo is the effective pressure, Pa the atmospheric pressure (~ 100 kPa) expressed in the same units as σ'vo and n an exponent that depends on the relative density of the ground (Figure 3).

where:

 

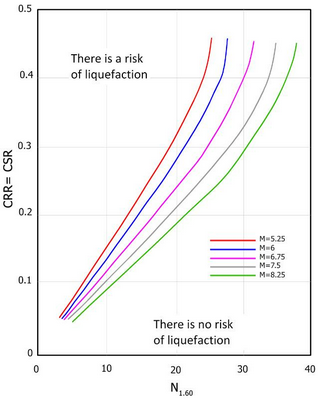
Figure 2 – Correlation between CRR and N1.60

 

 

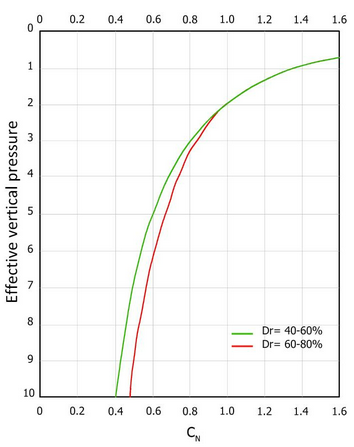
Figure 3 – Correction coefficient CN

 

It has been shown that an earthquake with a magnitude of 7.5 CRR can be expressed by the following:

 

 

Applying the following relationship is determined the liquefaction factor of safety FS:

 

 

if FS > 1,3 the deposit is non-liquefiable.

 

The authors pointed out that this procedure is valid for sands with D50 > 0.25 mm; for silty sands and silts they suggest further adjustment of the value of N1,60:

 

 

 

©  Geostru Software